今年の受験は Gröbner 基底で乗り切れ!
どうもみなさん今日は!突然ですが僕は受験数学が苦手です。しかし、代数幾何のGröbner(グレブナー)基底の理論 を学んでから、受験数学が全く苦にならなくなりました!今回は、まだ受験数学と格闘しなくてはならないみなさんの為に、受験に役立つGröbner基底 の紹介を、しちゃうゾ☆
直線と平面の問題
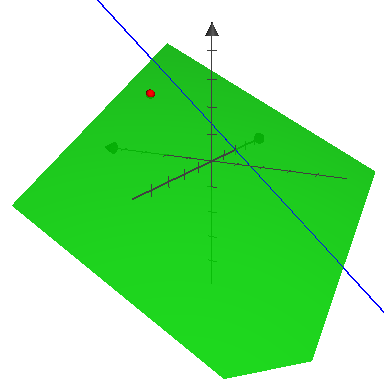
さてさて、まずは次の空間図形の問題を考えてみまっしょー。
問題.x , y , z x,y,z x , y , z ℓ : ( x , y , z ) = ( 0 , − 3 , − 2 ) + t ( 1 , 3 , 2 ) ( t ∈ R ) \ell:(x, y, z) = (0, -3, -2) + t(1,3,2)\quad (t
\in \mathbb{R}) ℓ : ( x , y , z ) = ( 0 , − 3 , − 2 ) + t ( 1 , 3 , 2 ) ( t ∈ R ) P ( 1 , 2 , 1 ) P(1,2,1) P ( 1 , 2 , 1 ) ℓ \ell ℓ P P P α \alpha α z z z R R R
うひゃあ、典型的な空間図形の問題ですね……!コワイ!
えっと、まず平面の式が必要で……直線 ℓ \ell ℓ A ( 0 , − 3 , 2 ) A(0,
-3, 2) A ( 0 , − 3 , 2 ) ( 1 , 3 , 2 ) (1,3,2) ( 1 , 3 , 2 ) α \alpha α P ( 1 , 2 , 1 ) P(1,2,1) P ( 1 , 2 , 1 ) t , s ∈ R t, s \in \R t , s ∈ R
A X ⃗ = t A P ⃗ + s A Q ⃗ ∴ O X ⃗ = O A ⃗ + A X ⃗ = O X ⃗ + t A P ⃗ + s A Q ⃗ = . . . = ( s + t , − 3 + 5 s + 3 t , − 2 + 3 s + 2 t )
\begin{aligned}
\vec{AX} &= t \vec{AP} + s\vec{AQ} \\
\therefore \vec{OX} &= \vec{OA} + \vec{AX}\\
&= \vec{OX} + t \vec{AP} + s\vec{AQ} \\
&= ... = (s+t, -3 + 5s + 3t, -2 + 3s + 2t)
\end{aligned}
A X ∴ OX = t A P + s A Q = O A + A X = OX + t A P + s A Q = ... = ( s + t , − 3 + 5 s + 3 t , − 2 + 3 s + 2 t )
だからええとこれが z z z = 0 =0 = 0 s + t = 0 , − 3 + 5 s + 3 t = 0 s + t = 0, -3 + 5s + 3t =
0 s + t = 0 , − 3 + 5 s + 3 t = 0
R ( 0 , 0 , − 1 2 ) R(0, 0, -\frac{1}{2}) R ( 0 , 0 , − 2 1 )
だ!!!とかやっちゃ、ダメ ですよ!?こういう時こそGröbner基底を使う んです!!
Gröbner基底っていうのは、多項式環のイデアルの都合のよい生成元のことです。ってどういうこと???多項式の零点で表される図形 」、イデアルの都合のよい生成元っていうのは「図形の性質が全て詰まっていてしかも扱い易い多項式 」のことだと思えばいいです。
では、さっそくやってみましょー。まずは、上の図形をイデアルに直すところからです。ℓ \ell ℓ I \mathfrak{I} I I = ⟨ x − t , y − ( 3 t − 3 ) , z − ( 2 t − 2 ) ⟩
\mathfrak{I} = \left\langle x-t, y - (3t - 3),z - (2t - 2) \right\rangle
I = ⟨ x − t , y − ( 3 t − 3 ) , z − ( 2 t − 2 ) ⟩ ℓ \ell ℓ
ℓ : ( x , y , z ) = ( 0 , − 3 , − 2 ) + t ( 1 , 3 , 2 ) = ( t , 3 t − 3 , 2 t − 2 ) \ell:(x, y, z) = (0, -3, -2) + t(1,3,2)
= (t, 3t - 3, 2t - 2) ℓ : ( x , y , z ) = ( 0 , − 3 , − 2 ) + t ( 1 , 3 , 2 ) = ( t , 3 t − 3 , 2 t − 2 )
つまり、x = t , y = 3 t − 3 , z = 2 t − 2 x = t, y = 3t - 3, z = 2t
-2 x = t , y = 3 t − 3 , z = 2 t − 2 ℓ \ell ℓ I \mathfrak{I} I = 0 =0 = 0
図形を表すイデアル = 定義式を = 0 =0 = 0
ということになります。同様に点 P P P J \mathfrak{J} J x = 1 , y = 2 , z = 1 x = 1, y = 2, z = 1 x = 1 , y = 2 , z = 1 = 0 =0 = 0 J = ⟨ x − 1 , y − 2 , z − 1 ⟩ \mathfrak{J} = \langle x - 1, y
- 2, z - 1 \rangle J = ⟨ x − 1 , y − 2 , z − 1 ⟩ J \mathfrak{J} J I \mathfrak{I} I J \mathfrak{J} J I J \mathfrak{I} \mathfrak{J} IJ
I J = ⟨ f g | f ∈ I , g ∈ J ⟩ \mathfrak{I} \mathfrak{J} = \left\langle
fg\ \middle|\ f \in \mathfrak{I}, g \in \mathfrak{J}
\right\rangle IJ = ⟨ f g ∣ f ∈ I , g ∈ J ⟩
ちょっと見なれないかもしれませんが、右辺の意味は、
それぞれのイデアル(図形)の要素を取ってきて、掛け合わせて得られる式全体のイデアル
ということです。どういうことか?上で見た I , J \mathfrak{I}, \mathfrak{J} I , J
I J = ⟨ ( x − 1 ) ( x − t ) , ( x − 1 ) ( y − ( 3 t − 3 ) ) , ( x − 1 ) ( z − ( 2 t − 2 ) ) , ( y − 2 ) ( x − t ) , ( y − 2 ) ( y − ( 3 t − 3 ) ) , … ⟩ \mathfrak{I}\mathfrak{J} = \langle (x -
1)(x - t), (x - 1)(y -(3t -3)), (x - 1)(z - (2t - 2)), (y - 2)(x - t),
(y - 2)(y-(3t -3)), \dots \rangle IJ = ⟨( x − 1 ) ( x − t ) , ( x − 1 ) ( y − ( 3 t − 3 )) , ( x − 1 ) ( z − ( 2 t − 2 )) , ( y − 2 ) ( x − t ) , ( y − 2 ) ( y − ( 3 t − 3 )) , … ⟩
ね、一つずつ取ってきて掛け合わせた 感じになってるでしょ?どうしてこうなるのか?そこはそれ、受験数学だからなるものはなります!
……と云ってしまってもいいですけど、いちおうちゃんと説明出来ます。そもそもイデアルというのは、「各要素がゼロになるような点全体の集合」なのでした。ところで、
( x − 1 ) ( y − ( 3 t − 3 ) ) = 0 (x - 1)(y -(3t -3))=0 ( x − 1 ) ( y − ( 3 t − 3 )) = 0
という方程式の意味は、直観的には「x − 1 = 0 x - 1 =
0 x − 1 = 0 y − ( 3 t − 3 ) = 0 y - (3t - 3) = 0 y − ( 3 t − 3 ) = 0
なって貰ったところで、もういちど虚心坦懐にイデアル I J \mathfrak{I}\mathfrak{J} IJ
I J = ⟨ ( x − 1 ) ( x − t ) , ( x − 1 ) ( y − ( 3 t − 3 ) ) , ( x − 1 ) ( z − ( 2 t − 2 ) ) , ( y − 2 ) ( x − t ) , ( y − 2 ) ( y − ( 3 t − 3 ) ) , … ⟩ \mathfrak{I}\mathfrak{J} = \langle (x -
1)(x - t), (x - 1)(y -(3t -3)), (x - 1)(z - (2t - 2)), (y - 2)(x - t),
(y - 2)(y-(3t -3)), \dots \rangle IJ = ⟨( x − 1 ) ( x − t ) , ( x − 1 ) ( y − ( 3 t − 3 )) , ( x − 1 ) ( z − ( 2 t − 2 )) , ( y − 2 ) ( x − t ) , ( y − 2 ) ( y − ( 3 t − 3 )) , … ⟩
ウゲエ、こんなのの何処に平面の情報が隠れているんダッι(`ロ´)ノ!
……とまあ、怒らないでください。これだけ見せられたら確かにウゲエっとなってしまうのもわかります。そこで、登場するのが
Gröbner基底 です!Gröbner基底 とは何か。都合のよい生成元だと云いましたね。「図形の性質が全て詰まっていてしかも扱い易い多項式」のことなのでした。では、Gröbner基底を早速計算してみましょう!
……ハイ、と云うことで、その計算結果がこちらになります。
I J = ⟨ x + y − 2 z − 1 , y z − 3 / 2 z 2 − y + 3 / 2 z , t z − 1 / 2 z 2 − t − 1 / 2 z + 1 , y 2 − 9 / 4 z 2 − 7 / 2 y + 21 / 4 z , t y − 3 / 4 z 2 − 2 t − 3 / 2 y + 7 / 4 z + 2 ⟩
\mathfrak{I}\mathfrak{J} = \langle x + y - 2z - 1,y z - 3/2 z^2 - y +
3/2 z,t z - 1/2 z^2 - t - 1/2 z + 1,y^2 - 9/4 z^2 - 7/2 y + 21/4 z,t y -
3/4 z^2 - 2t - 3/2 y + 7/4 z + 2 \rangle
IJ = ⟨ x + y − 2 z − 1 , yz − 3/2 z 2 − y + 3/2 z , t z − 1/2 z 2 − t − 1/2 z + 1 , y 2 − 9/4 z 2 − 7/2 y + 21/4 z , t y − 3/4 z 2 − 2 t − 3/2 y + 7/4 z + 2 ⟩
ウゲエ、何やら式がイッパイ……。しかし、良く見ると、x , y , z x, y, z x , y , z x + y − 2 z − 1 x + y - 2z - 1 x + y − 2 z − 1 = 0 =0 = 0 ℓ \ell ℓ P P P
x + y − 2 z − 1 = t + ( 3 t − 3 ) − 2 ( 2 t − 2 ) − 1 = 0 x + y - 2z -1 = t + (3t - 3) - 2(2t -
2) - 1 = 0 x + y − 2 z − 1 = t + ( 3 t − 3 ) − 2 ( 2 t − 2 ) − 1 = 0 x + y − 2 z − 1 = 1 + 2 − 2 1 ˙ − 1 = 0 x + y - 2z - 1 = 1 + 2
- 2 \dot 1 - 1 = 0 x + y − 2 z − 1 = 1 + 2 − 2 1 ˙ − 1 = 0
おお!見事に点 P P P ℓ \ell ℓ
あとは、これで x = y = 0 x = y = 0 x = y = 0
あるいは代入する代わりに、上で求めた平面 α \alpha α z z z z z z x = y = 0 x = y = 0 x = y = 0 ⟨ x , y , x + y − 2 z − 1 ⟩ \langle x, y, x + y - 2z - 1
\rangle ⟨ x , y , x + y − 2 z − 1 ⟩
⟨ z + 1 / 2 , y , x ⟩ \langle z + 1/2 ,y,x
\rangle ⟨ z + 1/2 , y , x ⟩
となり、一つ目の式から z = − 1 / 2 z = -1/2 z = − 1/2
Gröbner基底の計算方法
では、具体的にGröbner基底はどのように計算すればいいんでしょうか?幾つか方法を解説しますが、簡単な方法からやってみましょう。
皆さんは、受験生ですから、1変数の多項式の割り算は出来ますね?出来るとしましょう。それを多変数に拡張してやったような方法でやります。z 4 + 2 x + 3 x 2 y + z 3 y 2 z^4 +
2x + 3x^2y + z^3 y^2 z 4 + 2 x + 3 x 2 y + z 3 y 2 x , x 2 y , z 3 y 2 x, x^2y, z^3 y^2 x , x 2 y , z 3 y 2
まず、文字の間の大小関係を決めます。これは好きに決めて構いません。例えば
x > y > z x > y > z x > y > z
「大きな文字」をより沢山含んでいる方が大きい単項式とします。例えば
x 3 > x 2 x^3 > x^2 x 3 > x 2 x 2 > y 100 z 500 x^2 > y^{100}z^{500} x 2 > y 100 z 500
このようにして決めた単項式の順番に従って、文字式降冪の順に、つまり大きい方から順々に並べていってください。例えば、
z 4 + 2 x + 3 x 2 y + z 3 y 2 → 3 x 2 y + 2 x + y 2 z 3 + z 4 z^4 + 2x + 3x^2y + z^3 y^2 \to 3x^2y +
2x + y^2 z^3 + z^4 z 4 + 2 x + 3 x 2 y + z 3 y 2 → 3 x 2 y + 2 x + y 2 z 3 + z 4
のようになります。多項式 f f f L T ( f ) LT(f) L T ( f )
そして、遂に多項式の割り算に入ります。単項式の割り算と違うところは、割られる式に対して、複数の割る式が取れることです。つまり、
「x 2 y + x + y x ^2 y + x + y x 2 y + x + y x 2 − y x^2 - y x 2 − y x − y x
- y x − y
具体的に割る方法は、
割る式(g g g f 1 , f 2 , f 3 … f_1, f_2, f_3
\dots f 1 , f 2 , f 3 …
割る式の順番を決めて f 1 , f 2 , f 3 , … f_1, f_2, f_3,
\dots f 1 , f 2 , f 3 , … f i f_i f i q i q_i q i r r r
g g g s s s s s s f i f_i f i q , r q, r q , r もし割れる項がなければ、s s s r r r s s s
q i ← q i + q q_i \leftarrow q_i + q q i ← q i + q g g g s s s
こんな感じです。以下、式の集まり G = ⟨ g 1 , g 2 , … , g s ⟩ G =
\langle g_1, g_2, \dots, g_s\rangle G = ⟨ g 1 , g 2 , … , g s ⟩ f f f f ˉ G \bar{f}^G f ˉ G f , g f, g f , g S ( f , g ) S(f, g) S ( f , g )
S ( f , g ) = L C M ( L T ( f ) , L T ( g ) ) L T ( f ) f − L C M ( L T ( f ) ) L T ( g ) g S(f, g) = \frac{LCM(LT(f),
LT(g))}{LT(f)} f - \frac{LCM(LT(f))}{LT(g)} g S ( f , g ) = L T ( f ) L CM ( L T ( f ) , L T ( g )) f − L T ( g ) L CM ( L T ( f )) g
ここで、 L C M ( α , β ) LCM(\alpha, \beta) L CM ( α , β ) α , β \alpha, \beta α , β f , g f,g f , g 適当に足し引きして先頭項を打消し合わせた ものが S ( f , g ) S(f, g) S ( f , g ) L C M ( x 2 y z , x z 2 ) = x 2 y z 2 LCM(x^2yz, xz^2) = x^2yz^2 L CM ( x 2 yz , x z 2 ) = x 2 y z 2
これを踏まえると、イデアル I I I
G = I G = I G = I G G G f , g f, g f , g
s = S ( f , g ) ‾ G ≠ 0 s = \overline{S(f, g)}^G \neq 0 s = S ( f , g ) G = 0 G G G s s s もしどの二元に対しても S ( f , g ) ‾ G = 0 \overline{S(f,
g)}^G = 0 S ( f , g ) G = 0
こうして得られた G G G I I I Wikipedia
とかの計算法を見ればいいんじゃないですか。手計算が面倒なら、SINGULAR
という非常に優れたソフトウェアを使ってパソコンに計算を肩代わりさせることも出来ますし、Haskell
が使える人はぼくの作ったcomputational-algebra
ライブラリを使うといいかもしれません。
空間図形の問題2
次はこんな問題を考えてみましょー。
O O O O P ⃗ = s O A ⃗ + t O B ⃗ ( s , t ∈ R , で O , A , B は同一直線上にない ) \vec{OP} =
s\vec{OA} + t\vec{OB}\quad (s, t \in \mathbb{R}, \text{ で } O,A,B
\text{は同一直線上にない}) OP = s O A + t OB ( s , t ∈ R , で O , A , B は同一直線上にない ) s , t s, t s , t 3 s + 4 t = 2 3s +
4t = 2 3 s + 4 t = 2 P P P
えーっと、3 s + 4 t = 2 ⟺ 3 / 2 s + 2 t = 1 3s + 4t = 2 \iff 3/2 s + 2t =
1 3 s + 4 t = 2 ⟺ 3/2 s + 2 t = 1 s ′ = 3 / 2 s , t ′ = 2 t s' = 3/2s, t' =
2t s ′ = 3/2 s , t ′ = 2 t
O P ⃗ = s O A ⃗ + t O B ⃗ = s ′ ( 2 / 3 O A ⃗ ) + t ′ ( O B ⃗ / 2 ) \vec{OP} = s\vec{OA} + t\vec{OB} =
s' (2/3 \vec{OA}) + t' (\vec{OB}/2) OP = s O A + t OB = s ′ ( 2/3 O A ) + t ′ ( OB /2 )
だから……O A ′ ⃗ = 2 / 3 O A ⃗ , O B ′ ⃗ = O B ⃗ / 2 \vec{OA'} = 2/3 \vec{OA},
\vec{OB'} = \vec{OB}/2 O A ′ = 2/3 O A , O B ′ = OB /2 s ′ + t ′ = 1 s' + t' = 1 s ′ + t ′ = 1 P P P O A OA O A 2 : 1 2:1 2 : 1 O B OB OB
あーダサいダサいダサい!ダサ過ぎます!何で両辺 2 2 2
線分 O A OA O A 2 : 1 2:1 2 : 1 O B OB OB
ですか!具体的に式を答えろってんですよ、ええ。なんなら変数を消去して定義式を答えろってんです!だいいち、こんなのはGröbner基底をつかえば一発なんです!
明日もう一度ここに来て下さい。本物の変数消去を見せてあげますよ。
いや、明日じゃなくて今でいいんですけど。おきまりのようにイデアル
I I I O A ⃗ = ( a , c ) , O B ⃗ = ( b , d ) \vec{OA} = (a, c), \vec{OB} = (b, d) O A = ( a , c ) , OB = ( b , d )
I = ⟨ x − ( s a + t b ) , y − ( s c + t d ) , 3 s + 4 t − 2 ⟩ I = \langle x - (sa + tb), y - (sc +
td), 3s + 4t - 2 \rangle I = ⟨ x − ( s a + t b ) , y − ( sc + t d ) , 3 s + 4 t − 2 ⟩
これのGröbner基底を求めてやると……
I = ⟨ s + 4 / 3 t − 2 / 3 , c t − 3 / 4 d t − 1 / 2 c + 3 / 4 y , a t − 3 / 4 b t − 1 / 2 a + 3 / 4 x , − b c + a d + 2 c x − 3 / 2 d x − 2 a y + 3 / 2 b y ⟩ I = \langle s + 4/3 t - 2/3 ,c t - 3/4
d t - 1/2 c + 3/4 y,a t - 3/4 b t - 1/2 a + 3/4 x,-b c + a d + 2c x -
3/2 d x - 2a y + 3/2 b y \rangle I = ⟨ s + 4/3 t − 2/3 , c t − 3/4 d t − 1/2 c + 3/4 y , a t − 3/4 b t − 1/2 a + 3/4 x , − b c + a d + 2 c x − 3/2 d x − 2 a y + 3/2 b y ⟩
……お!最後の式− b c + a d + 2 c x − 3 / 2 d x − 2 a y + 3 / 2 b y -b c + a d + 2c x - 3/2 d x
- 2a y + 3/2 b y − b c + a d + 2 c x − 3/2 d x − 2 a y + 3/2 b y s , t s,
t s , t O A ⃗ \vec{OA} O A O B ⃗ \vec{OB} OB
|l、{
j} /,,ィ//| / ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ノ/ u {:}//ヘ | あ…ありのまま
今 起こった事を話すぜ! ,!V,ハ |
< 『おれはGröbner基底を計算していたとs , t s, t s , t
実は、「上手く順序の選んでGröbner基底を計算すると、その変数を消去出来る」という事実があります。ヒューッ!スゴイ!
つまり、パラメータを消去したいような式が与えられたら、
与えられた式から成るイデアルを作って、
消したい文字が大きくなるような順序で、
Gröbner基底を計算して、
その文字の出て来ない式をその基底の中から選ぶ。
というような手続を踏めば、一瞬でパラメータを消去出来るという寸法です。なんってこったい/(^o^)\。
勿論、数式が足りなかったり多すぎたりすると上手くいかないことがあって、そういう場合は
0 = 0 0 = 0 0 = 0 1 = 0 1 = 0 1 = 0
もっと変数消去
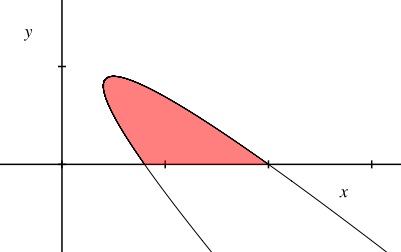
t t t { x = 1 + t 2 y = 2 − t − t 2 \begin{cases}
x &= 1 + t^2\\
y &= 2 - t - t^2
\end{cases}
{ x y = 1 + t 2 = 2 − t − t 2 x x x
面積はどうでもいいですけど、この曲線ってどんな曲線なんですかね?わたし、気になります!
という訳で、上で紹介した変数消去法を試してみましょー。I = ⟨ x − ( 1 + t 2 ) , y − ( 2 − t − t 2 ) ⟩ I = \langle x - (1 + t^2), y - (2 - t - t^2)
\rangle I = ⟨ x − ( 1 + t 2 ) , y − ( 2 − t − t 2 )⟩ t t t
x 2 + 2 x y + y 2 − 7 x − 6 y + 10 x^2 + 2x y + y^2 - 7x - 6y +
10 x 2 + 2 x y + y 2 − 7 x − 6 y + 10
が唯一の基底として得られます!これが定義方程式のようですね!グラフに描いてみると、
……?え?面積?パラメータ積分すればいいんと違う。
連立方程式の解
Gröbner基底が威力を発揮するのは、他にもあります!例えば、次のような連立方程式は受験でよく出て来ますね。
{ x 2 + y 2 = 16 x 3 + y 3 = 44
\begin{cases}
x^2+y^2 &= 16\\
x^3+y^3 &= 44
\end{cases}
{ x 2 + y 2 x 3 + y 3 = 16 = 44 x + y x + y x + y
これも、Gröbner基底を使えば一瞬です!今、知りたいのは x + y x + y x + y s s s x , y x, y x , y
I = ⟨ x 2 + y 2 − 16 , x 3 + y 3 − 44 , s − ( x + y ) ⟩
I = \langle x^2 + y^2 - 16,x^3 + y^3 - 44,s - (x + y) \rangle
I = ⟨ x 2 + y 2 − 16 , x 3 + y 3 − 44 , s − ( x + y )⟩
これのGröbner基底を計算して、 s s s
s 3 − 48 s + 88
s^3 - 48s + 88
s 3 − 48 s + 88
という式が得られました!この式 = 0 =0 = 0 s 3 − 48 s + 88 = ( s − 2 ) ( s 2 + 2 s − 44 ) = 0
s^3 - 48s + 88 = (s - 2)(s^2 + 2s -44) = 0
s 3 − 48 s + 88 = ( s − 2 ) ( s 2 + 2 s − 44 ) = 0 x , y ∈ R x, y \in \R x , y ∈ R s ∈ R s \in R s ∈ R s = 2 s = 2 s = 2
連立方程式の解ふたたび未遂
これと同様にして、
x = 7 + 5 2 3 , y = 7 − 5 2 3 x = \sqrt[3]{7+ 5\sqrt{2}}, y =
\sqrt[3]{7 - 5\sqrt{2}} x = 3 7 + 5 2 , y = 3 7 − 5 2 x 4 + y 4 , x 5 + y 5 x^4
+ y^4, x^5 + y^5 x 4 + y 4 , x 5 + y 5
というような問題も一瞬で解けます!というようなことを書こうと思ったんですが、自前のライブラリだと二十分経っても計算が終わらず、Singular
に計算させたところ、
I = ⟨ t 21 − 140 t 18 + 3098 t 15 + 4788 t 12 − 702391 t 9 + 3996104 t 6 + 2190656 t 3 − 175616 , 555268627200 s − 164581 t 20 + 22955732 t 17 − … ⟩ I = \langle
t^{21}-140t^{18}+3098t^{15}+4788t^{12}-702391t^{9}+3996104t^6+2190656t^3-175616,
555268627200s-164581t^{20}+22955732t^{17}- \dots \rangle I = ⟨ t 21 − 140 t 18 + 3098 t 15 + 4788 t 12 − 702391 t 9 + 3996104 t 6 + 2190656 t 3 − 175616 , 555268627200 s − 164581 t 20 + 22955732 t 17 − … ⟩
というホンにホンに懼ろしいイデアルが出来したので、諦めました。
極値問題ナンノソノ
なんかー、多項式のー、領域とかー、そんなんばっかんでー、飽きたんスけどー。
そんな声が聴こえてきました。よろしい、ならば極値問題だ 。
正の数 x , y , z x, y, z x , y , z 1 x + 1 y + 1 z = 6 \frac{1}{x} + \frac{1}{y} + \frac{1}{z} =
6 x 1 + y 1 + z 1 = 6 x + 2 y + 3 z x+ 2y +3z x + 2 y + 3 z
アーなんかこういうのよくありますよねハイ。求まったからといってナンナンジャイという感じですが、まあそれいったら御仕舞いなので。Lagrange の未定乗数法
という大学に入ると習う秘技がありまして、それは、
制約 f ( x , y , z ) = 0 f(x, y, z) = 0 f ( x , y , z ) = 0 g ( x , y , z ) g(x, y, z) g ( x , y , z )
という形式の問題を解く時には、連立方程式
{ ∂ λ { λ f ( x , y , z ) + g ( x , y , z ) } = 0 ∂ x { λ f ( x , y , z ) + g ( x , y , z ) } = 0 ∂ y { λ f ( x , y , z ) + g ( x , y , z ) } = 0 ∂ z { λ f ( x , y , z ) + g ( x , y , z ) } = 0
\begin{cases}
\partial_\lambda \left\{ \lambda f(x, y, z) + g(x, y, z) \right\} &=
0\\
\partial_x \left\{ \lambda f(x, y, z) + g(x, y, z) \right\} &= 0\\
\partial_y \left\{ \lambda f(x, y, z) + g(x, y, z) \right\} &= 0\\
\partial_z \left\{ \lambda f(x, y, z) + g(x, y, z) \right\} &= 0
\end{cases}
⎩ ⎨ ⎧ ∂ λ { λ f ( x , y , z ) + g ( x , y , z ) } ∂ x { λ f ( x , y , z ) + g ( x , y , z ) } ∂ y { λ f ( x , y , z ) + g ( x , y , z ) } ∂ z { λ f ( x , y , z ) + g ( x , y , z ) } = 0 = 0 = 0 = 0
の解を求めればよいというモノです。これを解いて、λ \lambda λ ∂ x , … \partial_x, \dots ∂ x , … x x x x x x x x x ∂ y \partial_y ∂ y ∂ λ \partial_\lambda ∂ λ
これと
Gröbner基底の合わせ技で、なな、なんと!この問題解けちゃいます!まず、制約式から
x , y , z ≠ 0 x, y, z \neq 0 x , y , z = 0 x y z xyz x yz f ( x , y , z ) = y z + 2 z x + 3 x y − 6 x y z f(x,y,z) = yz + 2zx +
3xy - 6xyz f ( x , y , z ) = yz + 2 z x + 3 x y − 6 x yz g ( x , y , z ) = x + 2 y + 3 z g(x,y,z) =
x+2y+3z g ( x , y , z ) = x + 2 y + 3 z
{ y z + 2 x z + 3 x y − 6 x y z = 0 2 λ z + 3 λ y + 1 = 0 λ z + 3 λ x + 2 = 0 λ y + 2 λ x + 3 = 0
\begin{cases}
yz + 2xz + 3 xy - 6xyz &= 0\\
2 \lambda z + 3 \lambda y + 1 &= 0\\
\lambda z + 3 \lambda x + 2 &= 0\\
\lambda y + 2 \lambda x + 3 &= 0
\end{cases}
⎩ ⎨ ⎧ yz + 2 x z + 3 x y − 6 x yz 2 λ z + 3 λ y + 1 λ z + 3 λ x + 2 λ y + 2 λ x + 3 = 0 = 0 = 0 = 0
となります。そこで、このイデアルを考えて、更にグレブナー基底を計算してやると、次のようになります。
I = ⟨ 9 z 3 − 18 z 2 + 11 z − 2 , y + 9 z 3 − 15 z 2 + 5 z , x + 2 y − 6 z 2 + 3 z , 4 λ − 27 x z 2 + 54 x z − 33 x − 54 y z 2 + 108 y z − 66 y + 81 z 3 − 180 z 2 + 135 z − 22 ⟩
I = \langle 9z^3-18z^2+11z-2, y+9z^3-15z^2+5z, x + 2y - 6z^2+3z,
4\lambda-27xz^2+54xz-33x-54yz^2+108yz-66y+81z^3-180z^2+135z-22\rangle
I = ⟨ 9 z 3 − 18 z 2 + 11 z − 2 , y + 9 z 3 − 15 z 2 + 5 z , x + 2 y − 6 z 2 + 3 z , 4 λ − 27 x z 2 + 54 x z − 33 x − 54 y z 2 + 108 yz − 66 y + 81 z 3 − 180 z 2 + 135 z − 22 ⟩
これをよく見ると……おっ!最初の式は z z z 9 z 3 − 18 z 2 + 11 z − 2 = ( z − 1 ) ( 3 z − 2 ) ( 3 z − 1 ) 9z^3 - 18z^2 + 11z - 2 = (z-1)(3 z - 2) (3 z
- 1) 9 z 3 − 18 z 2 + 11 z − 2 = ( z − 1 ) ( 3 z − 2 ) ( 3 z − 1 ) z = 1 , 2 / 3 , 1 / 3 z = 1, 2/3, 1/3 z = 1 , 2/3 , 1/3 y + 9 z 3 − 15 z 2 + 5 z = 0 , x + 2 y − 6 z 2 + 3 z = 0 y+9z^3-15z^2+5z =
0, x + 2y - 6z^2+3z = 0 y + 9 z 3 − 15 z 2 + 5 z = 0 , x + 2 y − 6 z 2 + 3 z = 0
( x , y , z ) = ( 1 , 1 , 1 ) , ( − 2 / 3 , 2 / 3 , 2 / 3 ) , ( 1 / 3 , − 1 / 3 , 1 / 3 )
(x,y,z) = (1,1,1), (-2/3, 2/3, 2/3), (1/3, -1/3, 1/3)
( x , y , z ) = ( 1 , 1 , 1 ) , ( − 2/3 , 2/3 , 2/3 ) , ( 1/3 , − 1/3 , 1/3 )
と云う三つの解の候補があります。条件から求めるべき x , y , z x, y, z x , y , z x + 2 y + 3 z x + 2y + 3z x + 2 y + 3 z 6 6 6 x = y = z = 1 x = y = z = 1 x = y = z = 1 6 6 6
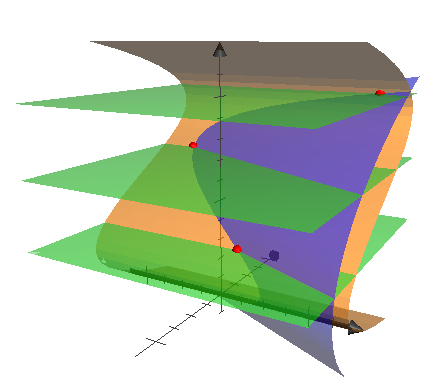
ちなみに、上のイデアルが表す図形は以下のような感じになっています(不要なので
λ \lambda λ
ちょうど三種類の曲面があって、それらの交点が上で求めた三つの解になっている訳です。つまり、条件付きの極値問題というのは、
これこれこういう図形の交点を求めてください!
という問題のことだったんだよ!な、なんだってー(AA略
極値その2
もっと簡単な、
x 2 + y 2 = 1 x^2+y^2=1 x 2 + y 2 = 1 x , y x, y x , y ( x + y ) ( 2 x − y ) (x+y)(2x - y) ( x + y ) ( 2 x − y )
といった問題についても、同様に計算すれば、
I = ⟨ 20 / 3 y 3 + x − 19 / 3 y , − 10 / 3 y 2 + λ + 13 / 6 , y 4 − y 2 + 1 / 40 ⟩ I = \langle 20/3 y^3 + x - 19/3 y,-10/3
y^2 + \lambda + 13/6 ,y^4 - y^2 + 1/40 \rangle I = ⟨ 20/3 y 3 + x − 19/3 y , − 10/3 y 2 + λ + 13/6 , y 4 − y 2 + 1/40 ⟩
となって、最後の多項式はみなさんもお馴染の複二次式ですから、y 2 y^2 y 2
三角関数の計算問題
たしかに Gröbner基底すごそうだけど、多項式だけじゃーん。
という声が聴こえてきました。では、ちょっと毛並みを変えて、今度は三角関数の絡んだ問題を解いてみましょう……!
sin x + cos y = 1 / 2 , cos x + sin y = 1 / 3 \sin x + \cos y = 1/2, \cos x + \sin y =
1/3 sin x + cos y = 1/2 , cos x + sin y = 1/3 sin ( x + y ) \sin(x + y) sin ( x + y )
t = sin x , u = cos y , s = cos x , v = sin y t = \sin x, u = \cos y, s = \cos x, v =
\sin y t = sin x , u = cos y , s = cos x , v = sin y sin 2 + cos 2 = 1 \sin^2 + \cos^2 = 1 sin 2 + cos 2 = 1 t 2 + s 2 = 1 , u 2 + v 2 = 1 t^2 + s^2 = 1, u^2 + v^2 = 1 t 2 + s 2 = 1 , u 2 + v 2 = 1 sin ( x + y ) = sin x cos y + cos x sin y = t u + s v \sin(x+y) =
\sin x \cos y + \cos x \sin y = tu + sv sin ( x + y ) = sin x cos y + cos x sin y = t u + s v I = { t + u − 1 2 , s + v − 1 3 , t 2 + s 2 − 1 , u 2 + v 2 − 1 }
\mathcal{I} = \left\{t + u - \frac{1}{2}, s + v - \frac{1}{3}, t^2 +
s^2 - 1, u^2 + v^2 - 1\right\}
I = { t + u − 2 1 , s + v − 3 1 , t 2 + s 2 − 1 , u 2 + v 2 − 1 } G = ⟨ g 1 , g 2 , g 3 , g 4 ⟩ = ⟨ u + 2 3 v − 13 36 , t − 2 3 v − 5 36 , s + v − 1 3 , v 2 − 1 3 v − 1127 1872 ⟩
G = \langle g_1, g_2, g_3, g_4 \rangle = \langle u + \frac{2}{3} v -
\frac{13}{36} ,t - \frac{2}{3} v - \frac{5}{36} ,s + v - \frac{1}{3}
,v^2 - \frac{1}{3} v - \frac{1127}{1872} \rangle
G = ⟨ g 1 , g 2 , g 3 , g 4 ⟩ = ⟨ u + 3 2 v − 36 13 , t − 3 2 v − 36 5 , s + v − 3 1 , v 2 − 3 1 v − 1872 1127 ⟩
t u + s v = g 1 t − g 2 2 / 3 v + 13 / 36 + g 3 v − g 4 ( 13 / 9 ) + ( − 59 / 72 ) tu + sv = g_1 t - g_2 2/3 v + 13/36 +
g_3 v - g_4 (13/9) + (-59/72) t u + s v = g 1 t − g 2 2/3 v + 13/36 + g 3 v − g 4 ( 13/9 ) + ( − 59/72 )
いいかんじに有理数の余り − 59 / 22 -59/22 − 59/22
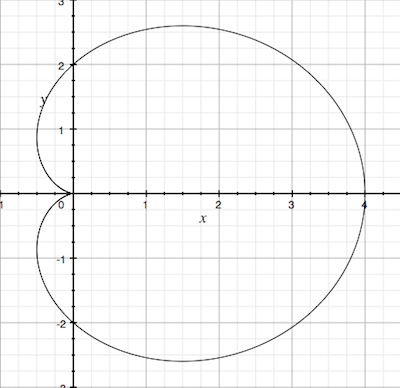
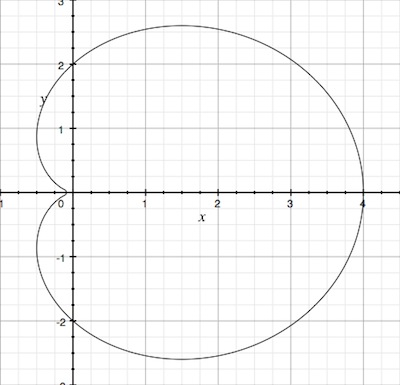
カージオイド
最後に、今までの手法を幾つか組み合わせて受験数学の有名問題を解いてみましょう。
r = a ( 1 + cos θ ) r = a(1 + \cos \theta) r = a ( 1 + cos θ )
曲線があるらしいです。カージオイド (心臓形)と呼ばれる曲線ですね。「曲線がある」で終わっているのは、まあ、どういう問題が出たか忘れたからです。もう四年前だから覚えてる訳なんてないですね!
問題を忘れてしまったので、じゃあとりあえず、「この極座標表示を x , y x, y x , y
{ x = r cos θ y = r sin θ r 2 = x 2 + y 2 θ = arctan ( y / x )
\begin{cases}
x &= r \cos\theta\\
y &= r \sin\theta\\
r^2 &= x^2 + y^2\\
\theta &= \arctan(y/x)
\end{cases}
⎩ ⎨ ⎧ x y r 2 θ = r cos θ = r sin θ = x 2 + y 2 = arctan ( y / x )
で表される座標系でした。この関係式を使って、上の曲線の方程式から
r , θ r, \theta r , θ sin θ , cos θ \sin
\theta, \cos \theta sin θ , cos θ θ \theta θ s = sin θ , c = cos θ s = \sin \theta, c = \cos \theta s = sin θ , c = cos θ r , s , c r, s, c r , s , c
座標変換や sin , cos \sin, \cos sin , cos
I = ⟨ r − a ( 1 + cos θ ) , x − r c , y − r s , r 2 − ( x 2 + y 2 ) ⟩
I = \langle r - a(1 + \cos \theta), x - rc, y - rs, r^2-(x^2+y^2)
\rangle
I = ⟨ r − a ( 1 + cos θ ) , x − rc , y − rs , r 2 − ( x 2 + y 2 )⟩
s 2 + c 2 = 1 s^2+c^2=1 s 2 + c 2 = 1 x = r c , y = r c , r 2 − ( x 2 + y 2 ) x =
rc, y = rc, r^2 -(x^2+y^2) x = rc , y = rc , r 2 − ( x 2 + y 2 ) a , x , y a,
x, y a , x , y 2 a x 3 − x 4 + a 2 y 2 + 2 a x y 2 − 2 x 2 y 2 − y 4
2a x^3 - x^4 + a^2 y^2 + 2a x y^2 - 2x^2 y^2 - y^4
2 a x 3 − x 4 + a 2 y 2 + 2 a x y 2 − 2 x 2 y 2 − y 4
が該当しそうです!グラフを描いてみると、この多項式の零点の図形は、確かにカージオイドを描くことが判りました!
なんか原点周りの曲線がちょっと粗いように見えますが、これはグラフ計算機の近似計算のせいで描画がおいついていないだけです。拡大してみると、ちゃんとなってるのがわかります。
おわりに
Gröbner基底すごいぞ〜受験数学とけるぞ〜という話でした。ベクトルの幾何の問題や連立方程式の問題は、コンピュータでGröbner基底を計算すればアッという間に解けるので、この冬はGröbner基底を覚えて他の受験生と差を付けよう!