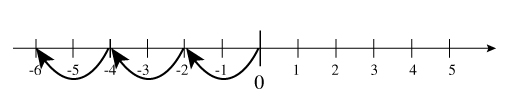絶対に理解出来ないモナドチュートリアル konn-san.com

足し算、引き算、掛け算

ところでちょっと小学校の頃のことを思い出してみよう。算数の時間。僕たちは足し算や掛け算を随分と長い時間を掛けて習ったものだった。たとえば「$1 + 1 = 2$」はこんな感じに習った：

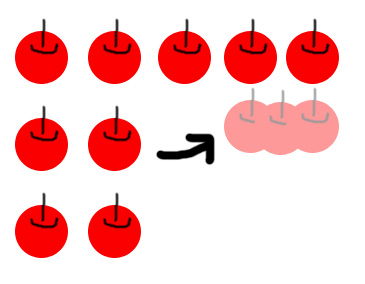
問：$1+1=?$

答：えーと、一つのりんごと一つのりんごを合わせて……

二つ！

じゃあ「$2 \times 3 = 6$」はこんな感じだ：

答：えーと、りんごを一列に二つずつ、計三列ならべればいいから……

六つ！

どんどん行こう。$5-3=2$。

答：五つのりんごから、三つ取って食べると……

二つ！

こんな具合に僕達は小学校で計算を身に付けていって、中学に入学する。 中学で早速、つぎのような問題にでくわして面喰うことになる。

問：$3 - 5 = ?$
三個のりんごから五個のりんごを……取れない！？

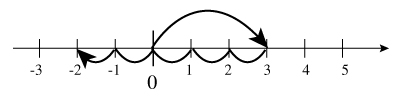
ここで颯爽と「負の数」が登場して、僕たちは引き算が出来るようになる。その時に、今度は数直線とかいうのがでてきて、

ゼロからスタートして右に三つ、左に五つ進んだところ。つまり答えは $-2$！

という感じに、「数直線をどっちに進むか」というような直観に基づいて負の数の演算を身に付ける。あるいは、「お財布に三百円しかないときに、五百円のおかしを買おうと思ったら、二百円だれかから借金しなくてはいけない」のように、借金のメタファで理解することもある。

これなら、掛け算だって出来る。$(-2) \times 3 = -6$。

マイナス掛けるマイナスはどうすればいいんだろう？というときには、今度は自動車の速度を云っているのだと思えばよい。そうすると $(-2) \times (-3) = 6$ は、

時速 $2$ km でバックする車が三時間前にいた位置は……$6$ km 先！

といった具合に計算することが出来るようになる。

小学校はもう卒業したんだけど？

……うん。云いたいことはわかる。この記事はさんすうのおべんきょう記事ではなくて、モナドチュートリアルだった筈だ。

　 |l､{　 　j}　/,,ｨ//｜　　　　　／￣￣￣￣￣￣￣￣￣￣￣￣￣￣￣￣￣￣￣￣
　 i|:!ヾ､ﾉ／ u {:}//ﾍ　　　　　|　あ…ありのまま 今　起こった事を話すぜ！
　 |ﾘ u’ }　 ,ﾉ　,!V,ﾊ |　　 　 ＜　『おれはモナドチュートリアルを読んでいたと
　 fト､{ﾙ{,ィ’ｅﾗ　, ﾀ人.　　　|　　思ったらいつのまにか算数の勉強をしていた』
　ヾ|宀| {´,)⌒`/ |<ヽﾄiゝ　　　|　型クラスだと圏論かだとか
　　ヽ iLﾚ 　u’ |　| ヾｌﾄﾊ〉.　|　そんなチャチなもんじゃあ　断じてねえ
　　 ﾊ !ニ⊇　‘／:} 　V:::::ヽ.　│　もっと恐ろしいものの片鱗を味わったぜ…
　 /:::丶’T’’ ／u’　_ /:::::::/｀ヽ ＼＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿²

その通り。でもこれからちゃんとモナドチュートリアルになる予定だから、安心してほしい。

じゃあ何で算数の話をしたのか？こんな記事を読んでいるくらいだから、多分、上でやったような算数はおちゃの子さいさいだと思う。$1 + 1$ だとか $(-2) \times (-3)$ だとか、こんなのは一瞬で計算出来ちゃうよね。じゃあ、そのおちゃの子さいさいの計算をするときに、上でやったようにいちいちリンゴとか数直線を思い浮かべて計算してるだろうか？

多分、答えはノーだと思う。小学校や中学校で習った最初のうちは、上に描いたような絵を頭に思い浮かべたり、指を折ったりしながらがんばって数えて答えを出していただろう。でも、今はそうじゃない。なんでだろう？

それは、何度も計算して慣れたからだ。小学校のころには宿題でひたすら計算ドリルとかが出されるし、掛け算に至っては九九を暗記するまで暗唱テストをされたりする。僕が小学校の頃には、ちょうど百マス計算とかいうのがはやって、10 × 10 のマスをひたすら埋めたものだ。そんな風にして、僕らは最初に与えられたリンゴだの速度だの直線上の距離だの、そういった意味を忘れて数の計算が出来るようになった。

もちろん、算数や数学を勉強する上で、前の章でやったような具体的なイメージを持つことはある程度意味があるし、理解の足しにもなる。でも、リンゴのイメージは負の数が導入されたときにむしろ理解の妨げになるし、借金のイメージは負の数どうしの掛け算にはうまく使えない。更に、高校に入って虚数が導入されたりしたら、直線のアナロジーはまったく利かなくなってしまう。そんなこんなで「ゼロより小さいってなんだよ……」とか、「自乗して負になるとかそんな数ないだろ……」とか云いながらも、嫌々計算している内に何となく計算が出来るようになっていく。

僕は、モナドにも同じことが云えると思う。世の中には色々な比喩（ブリトー、ベルトコンベア、箱、etc, etc…）を用いたモナドの説明がある。それぞれ、モナドについてのインスピレーションを与えてくれるし、理解する上で補助になることもある。でも、一つのイメージにだけ頼っていては理解出来ないことも沢山ある。IO モナドはなるほどベルトコンベアーのような気がする。でも、リストモナドのどこがベルトコンベアなんだ？逆に、リストはなるほどプログラマブルなコンテナかもしれないけど、IO のどこがコンテナなんだろう？もちろん、どちらもそれなりに説得力のある方法で、ほら、これはベルトコンベアでしょ、とか、コンテナでしょ、と云う風に説明することは出来るだろう。でも、説明が必要な時点で、それはそのイメージだけではモナドを説明し切れないということを意味しているんじゃないかな。

これは、「イメージに頼った説明を使うな」と貶しているのではない。何度もいったように、モナドの例を幾つか理解していく上では、そうした説明はとても役に立つ。でも、数とリンゴを対応させていたのでは負の数を受け容れられないように、イメージは時として適用範囲外への理解を却って阻害することもよくある。だから、モナドを理解したいと思ったら、そうしたイメージに助けを借りつつ、計算練習のように色々なモナドを使ったコードを書いていくことも同じくらい、あるいはそれ以上に大事なことだ。

モナドとはなにか

でも、じゃあモナドは何なの？と訊かれるかもしれない。これは難しい問だ。とはいっても簡単な答えを見付けることはできる：

モナドとは、モナドだ。

……これじゃ何も云ってない。その通り。そこで、お誂え向きに計算機科学者が通り掛かったので訊いてみよう。モナドって何ですか？

モナドは単なる自己関手の圏におけるモノイド対象だよ。何か問題でも？

まったくその通り。でも何を云ってるんだ？ふざけてるのか？という感じだ。困ったなあ。そこで、Twitter にいたちょっと頭におぼえのある人に訊いてみることにした。

型 m : * → * と合成演算 (>=>) :: (a → m b) → (b → m c) → a → m c と函数 return :: a → m aの組がモナドであるとは、次の法則を満たすことである：

1. f >=> (g >=> h) == (f >=> g) >=> h
2. f >=> return == f
3. return >=> f == f

……だから何なの？結局モナドってなんなんだ！ι(｀ロ´)ノ

無理もない。だって、「足し算って何？」って訊かれたら、どう答える？「足し算は……足し算だよ」としか答えようがないんじゃないかな？困ったなあと思って数学者に訊いてみたら、「何の足し算かによるけど」、と前置きして次のアーベル群の公理を述べると思う。

演算 $+$ が足し算であるとは、ある特別な数 $0$ があって、次の法則を満たすことである：

1. $a + (b + c) = (a + b) + c$
2. $a + 0 = a$
3. $0 + a = a$
4. どんな $a$ に対しても $(-a)$ という数があって、$a + (-a) = (-a) + a = 0$
5. $a + b = b + a$

でも、こんなことを云われても、チットモ足し算とは何かということが判ったような気はしない。でも、そんな事に関係なく、僕達は日頃から足し算をするし、必要とあれば掛け算や割り算だってする。それも、「十人で登山に行ったのに五人しか帰ってこない……」とか「宴会、十人で予約したけど二十人くらい来そうだ:;(∩´﹏`∩);:」とか「あー今日の宴会金足りないからあいつから1000円借りなきゃ」「二つずつお土産を買うから、全員分で十個だなー」とか、色々な場面、色々な局面で計算をしている。これらはみんな意味合いは違うど、同じ足し算掛け算で、僕たちは不自由なくそれを適用して使って、足し算をわかったような気になっている。

つまり、「モナドとは何か」ということの専門的な答えは理解しなくても、「モナドをどう使うか」という実際的な答えさえわかれば、僕らはそれを使うことは出来る。そうして使っている内に、どうやら俺はモナドがわかったぞ、という気分になって縦横無尽に使いこなせるようになる。「モナドとは何か」を知らずに、「モナドとはモナドである」という説明をいつしか自然と受け容れて使う。それが、プログラミングにおいて「モナドを理解する」ということだろう。

だから、繰り返しになるけど、プログラミングにおけるモナドを理解したかったら、チュートリアルを片手に試行錯誤して、とにかくいっぱいコードを読み書きするのが一番の近道だと思う。だって、算数の勉強だってそうしたんだし。OOP から来た人だって、クラスだのオブジェクトだの継承だの多態だのといった概念を、入門書の説明を読んだだけで理解してしまったという人は稀だろうと思う。色んなプログラムを書く内に覚えたんじゃないだろうか。初心者のうちは、for 文だの if 文だのだって何十回と書いてやっと使い方を覚えることだってよくある。だから、モナドも同じだ。その為に必要なモナドチュートリアルは、世の中に沢山あるんだし。そうしたチュートリアルを拠り所に、「モナドはモナドだ」と云えるようになるまであれこれとコードを書いてみる。それがモナドを理解するための唯一の道だ。

……「じゃあ数学的にはモナドとはどういう概念なのか？」って？ようこそ！ぜひ圏論を勉強してみよう。というか僕も今正に勉強しているところだ。圏論は、数学の様々な抽象化の方法が詰まった道具箱だ。その全てがプログラミングに応用出来るわけではないけど、知っておけば必ずプラスになる。とはいっても、圏論の議論は非常に抽象的なので、あるていど数学の基本的な議論や集合・論理の言葉に慣れてからでないと躓いてしまうところもある。プログラミングに使えるところだけつまみぐいしたい、という気持ちもわかる。でも、基本的な方法を押さえずにいきなり圏論に挑むのは、カレーも唐辛子も食べたことがないひとがいきなりハバネロを食べるようなものだ。あくまで一例だけれど、次のような本を読んでみると良いと思う。

結城浩『数学ガール』シリーズ

数学の面白さ、方法論を、軽い小説に載せて主人公たちと一緒に成長しながら学べる良著。集合や論理の基礎をしっかりとやる、というよりは、数学のやり方をこの本を通して身に付けるという用途がよいかも。

中内伸光『数学の基礎体力をつけるためのろんりの練習帳』

数学の論理と集合の基礎を、学ぶ上での心構えからていねいに説明した本。「ろんり」というのはこの著者の用語で、数学の基礎体力としての集合・論理のことです。著者独特のセンスの光る駄洒落が随所にちりばめられており、肩肘はらずに独習出来ます。僕は中学のときにこの本で勉強しました。また、こちらは未読ですが、同じ著者による『ろんりと集合』というのも良著のようです。

嘉田勝『論理と集合から始める数学の基礎』

集合と論理の使い方を懇切丁寧に紹介している良著。とのこと。とのこと、というのは私が未読だからですが、非常に評判が良い本ですので安心してお勧め出来ると思います。

こうした本で準備体操をして、圏論を勉強していくと、上で言及したような「モナドの法則」こそがモナドなのだということがわかるようになると思う。モナド則だけ並べられてもよくわからないけど、重要なのは、「モナドを使うと副作用の大半を統一的に扱うことができる」ということだ。モナドを始めとして、数学における代数的な構造というものは、その計算法則こそがその意味なのだ、ということは、多分数学をやっている内に腑に落ちてきて、プログラミング的なモナドの理解と、数学的なモナドの理解が一致するだろうと思う。

おまけ：モナドは命令書だ──未だ書かれぬ Yet Another Monad Tutorial へ向けて

さて、ここまでモナドは「書くしかない」という事をずっといってきた訳だけど、折角なのでちょっとだけ僕も「モナドチュートリアル」を書いてみようと思う。もう既に沢山あるし、モナドチュートリアルだけは絶対に書かないぞと思っていたのだけど、思い付いちゃったものは仕方がない。許してほしい。

と、いっても、なんだかもう眠いので、コード・サンプルとかはないし、試案のアウトラインだけを述べることにする。いうなれば予告編だ。

ここでは、幾分趣味に走った書き方をしているし、上でも云ったようにあくまで特殊な一例に過ぎない。ただ、他のチュートリアルと一緒に、この文章もちょっとだけでも理解の足しになってくれたら幸いだ。もし難しく感じたら、それはモナドが難しいということではなくて（いや、難しいのだけど、それは他のプログラミング手法と同じくらいの難しさだ）僕の書き方が不味いということ。それにアウトラインだけだし。だから、あ、わからんわ、と思ったらどんどん飛ばしてしまって構わない。

さて、モナドとは何か。僕は命令書、それも合成の出来る命令書だと云いたい。

どういう事か？そもそもモナドは、主に函数型プログラミングの世界での手法なのだった。よく「Haskell は副作用を許さない純粋函数型言語だからモナドが必要になる」といった説明を見かける。でも、これは正しくない。なぜなら、OCaml や Scala といった純粋ではない、副作用を許す函数型言語でも、モナドは便利に用いられているからだ。

何故これらの言語でモナドが使われているのだろうか？それには、そもそも函数型プログラミングとはどういうプログラミング・パラダイムなのかを考えてみる必要がある。よくある説明は「函数が第一級の対象として扱える」「代数的データ型を持つ」「再帰函数を基本としている」などだ。でもこれらは、函数型プログラミングの目標を達成するための手段に過ぎない、と僕は思う。

函数型プログラミングの目的。それは合成可能性、モジュラリティだ。その為に、函数型言語の基本は「函数の合成」に置かれている。函数合成こそ、函数型プログラミングの本質だ。プログラムを幾つもの小さな部品 = 函数に分割して、それらを貼り合わせて一つの大きなプログラムを作る。個々の部品は他の用途にも色々と使い回すことが出来る。それが函数型プログラミングの根底にある方法論だ。

なぜ関数合成が大事なのか、ということは他の記事でも散々議論されているのでこの辺りで終わりにするとしよう。

さて、モナドだ。

先程、モナドは「合成可能な命令書だ」と云った。あるいは「合成可能な設計図」と云ってもよい。この「合成出来る」というのが大事だ。モナドは、たちの悪い副作用を巧いこと合成するための枠組みなのだ。また、副作用そのものではなく、「命令書」あるいは「設計図」であるということが大事だ。

しかし、「設計図」とはいっても、リストモナドだとか Writer とか Reader とかいうのはその場ですぐに実行してしまっているように見える。だから、より設計図らしい例として、自由モナドというものを考えてみる。何だかいかめしい感じがするけど、ここではそういう名前のものがある、という感じでいい。

自由モナドというのは、ある特定のモナドのことを指すのではなくて、用意された道具立てからモナドを作る方法のことを指す。

「自由」というのは、「余分な法則から自由」ということ。自由モナドは、与えられた「命令のもと」から、命令書を自動的に作り出す方法だ。どんな感じなのか、ちょっとみてみよう。以下の例を見れば、モナドは命令書・設計図である、ということは容易に納得してもらえる筈だ……。

……と書いたところで、時間切れ。眠い。もうだめだ。まあ、試案のアウトラインということで、どういう戦略なのか書き下したい。

• モナドは合成可能な命令書であること
• 自由モナドを用いたプログラミングは、命令書を組み立てて、それを後から実行することに相当する。
• 実は、全てのモナドは自由モナドをつくって、そいつを適当に「実行」することで作ることが出来る
  • 自由モナドがプログラムのソースコードで、それを実行する「処理系」を色々に書くことで色んな計算が出来る！インタプリタを書くようなもの！
• モナドは怖くなかった！

といったような流れで、モナドは命令書であるということが相当の説得力を持って結論される予定であった。もちろん、モナドはモナドなんだけどね。サンプルコードなどが用意できたら、機会を改めて書きたい。あと、途中で書くことを断念したもう一つの理由は、自由モナドよりも手軽にモナド命令書を作れるOperational モナドというのもあるらしいということを知ったからで、これを検討してからの方がいいかなぁ、などと思ったのであった。

ただ、なにぶん筆不精なもので、多分書かれるのは当分先になるか、あるいはふみさんが先に書いて下さるかもしれない。書いてくれるといいなあ。僕はまだ自由モナドや Operational モナドをちゃんと使ったことがないので……。

まあいずれにせよ、モナドは合成可能な命令書であるということに主眼を置いて、そのことを学ぶ方法として、自由モナドなり Operational モナドなりで実際にモナドを作ってみる、というようなチュートリアルは、あってもよいのではないだろうか。という試案をここに述べておく。

おわりに

長々と書き散らしてしまったけど、いいたいことは以下の三つに尽きる：

• チュートリアルを読んだら、コードを書こう！
• チュートリアルのイメージに引きずられすぎてはいけない！
• モナドはモナドだ！コードを書こう！

以上！チュートリアルを読んだだけでは絶対にモナドはわからない。でも、それは他のプログラミング概念も同じこと。だから、気長に、腰を据えて、モナドなコードを書こう！

Have a Happy Monadic-Life!